💡 Idee: Suche iterativ eine zu \(A=A_0\) ähnliche (gleiche Eigenwerte) Matrix \(A_k\) , die wir mittels der QR-Zerlegung in eine obere Dreiecksmatrix \(R\) überführen können:
\[
A_k \to R = \begin{pmatrix} \lambda_1 & * & \cdots & * \\ & \lambda_2 & \ddots & \vdots \\ & & \ddots & * \\ & & & \lambda_N \end{pmatrix},
Q_k \to I_N
\]
Somit lassen sich die Eigenwerte von \(A_k\) (\(k \to \infty\) ) auf der Diagonalen ablesen (bzw. approximieren).
⚠️ Problem: Normale QR-Zerlegung mit \(A_{k+1} = R_k Q_k\) benötigt \(O(N^3)\) Operationen.
Hessenberg-Matrix
\[
H = \begin{pmatrix}
* & * & * & * & * \\
* & * & * & * & * \\
0 & * & * & * & * \\
0 & 0 & * & * & * \\
0 & 0 & 0 & * & *
\end{pmatrix}
\]
Eine Matrix \(H \in \mathbb{R}^{N \times N}\) heißt (obere) Hessenberg-Matrix, wenn \(H[n+2:N, n] = 0_{N-n-1}\) für \(n = 1,...,N-2\) gilt.
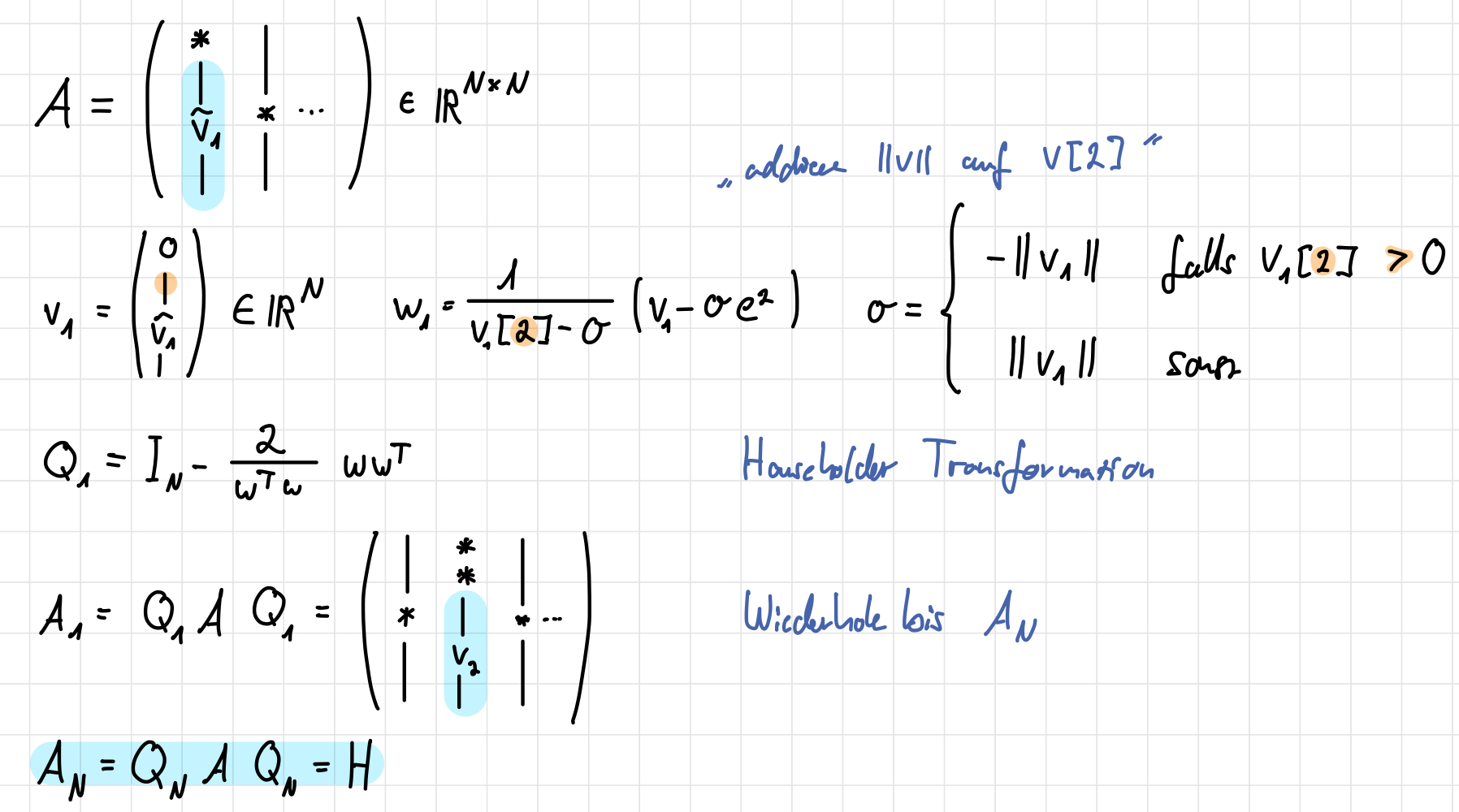
Sei \(A \in \mathbb{R}^{N \times N}\) . Dann existiert eine orthogonale Matrix \(Q \in \mathbb{R}^{N \times N}\) , so dass \[
H = QAQ^{\top}
\] eine Hessenberg-Matrix ist.
Die Berechnung von \(Q\) benötigt \(O(N^3)\) Operationen.
= np.array([8 , 12 / 5 , - 9 / 5 ],12 / 5 , 109 / 25 , 12 / 25 ],- 9 / 5 , 12 / 25 , 116 / 25 ]print (H := scipy.linalg.hessenberg(A))print (np.linalg.eig(A).eigenvalues)print (np.linalg.eig(H).eigenvalues)
[[8 -3 0]
[-3 4 0]
[0 0 5]]
[2244241/233640 559439/233640 5]
[2244241/233640 559439/233640 5]
Inverse Iteration mit Shift
Sei \(A \in \mathbb{R}^{N \times N}\) symmetrisch .
Wähle \(v^0 \in \mathbb{R}^N\) mit \(|v^0| = 1\) . \(k := 0\) und wähle \(\varepsilon > 0\) .
Berechne \[
\mu_k = r(A, v^k) = \frac{v^{\top} A v}{v^{\top} v},
\] . \(|Av^k - \mu_k v^k| < \varepsilon\) : STOP.
Berechne \[\begin{align*}
w^k &= (A - \mu_k I_N)^{-1}v^k, \\
v^{k+1} &= \frac{1}{|w^k|}w^k.
\end{align*}\]
Setze \(k := k + 1\) und gehe zu 1. .
\(r(A, w) \approx \lambda\)
QR-Iteration mit Shift
💡 Idee: Transformiere \(A\) auf ähnliche Hessenbergform \(H\) und führe die QR-Zerlegung mit Shift in \(O(N^2)\) durch.
Im Folgenden sei \(H \in \mathbb{R}^{N \times N}\) symmetrisch, tridiagonal und irreduzibel (\(H\) kann z.B. eine Hessenberg-Matrix sein).
Wähle \(\varepsilon \geq 0\) , setze \(H_0 = H\) , \(k := 0\) und \(n=N\) .
Falls \(|H_k[n, n-1]| \leq \varepsilon\) \(n := n - 1\) , \(n = 1\) : STOP
Wähle \(\mu_k = H[n, n]\) .
Berechne eine QR-Zerlegung \(H_k - \mu_k I_N = Q_k R_k\) .
Setze \(H_{k+1} = R_k Q_k + \mu_k I_N\) . \(k := k + 1\) , gehe zu 1 .
Es gilt \[\begin{alignat*}{2}
H_{k+1} &= R_k Q_k &&+ \mu_k I_N \\
&= Q_k^\top (A_k - \mu_k I_N) Q_k &&+ \mu_k I_N \\
&= Q_k^\top A_k Q_k
\end{alignat*}\]