7 Polynom-Interpolation
Gegeben sei eine Menge von Stützstellen \(\xi_0, \ldots, \xi_N\) und die zugehörigen Funktionswerte \(f_0, \ldots, f_N\).
🏁 Ziel: Finde eine Funktion \(f(\xi_n) = f_n\) für alle \(n = 0, \ldots, N\).
Im Folgenden betrachten wir verschiedene Darstellungsformen der Polynomen-Basis.
7.1 Monomenbasis
\[ P(t) = \sum_{n=0}^N a_n \cdot t^n \]
Zum Lösen der Interpolationsaufgabe muss der Koeffizientenvektor \(a = [a₀;a₁; \ldots ;a_N] \in \mathbb{R}^{N+1}\) bestimmt werden, welcher \[a₀+a₁ξ_n + a₂ξ_n^2 + \ldots + a_Nξ_n^N = f_n\] für \(n = 0, \ldots, N\) genügt. Dies führt auf ein lineares Gleichungssystem \(Ta = f\) mit \(f = [f₀; \ldots; f_N] \in \mathbb{R}^{N+1}\) und der Vandermonde-Matrix \[T = (ξ_n^k)_{n,k=0,\ldots,N} = \begin{pmatrix} 1 & ξ_0 & ξ_0^2 & \ldots & ξ_0^N \\ 1 & ξ_1 & ξ_1^2 & \ldots & ξ_1^N \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & ξ_N & ξ_N^2 & \ldots & ξ_N^N \end{pmatrix} \in \mathbb{R}^{(N+1) \times (N+1)}.\] Diese Matrix ist zwar regulär (da die \(ξ_n\) paarweise verschieden sind), hat aber in der Regel eine sehr schlechte Kondition.
7.2 Lagrange-Darstellung
Eine andere Möglichkeit ist die Darstellung über die Lagrange Basispolynome \(L_k \in \mathbb{P}_N\) mit \[L_n(t) = \prod_{\substack{k=0 \\ k \neq n}}^N \frac{t - ξ_k}{ξ_n - ξ_k}.\] Dadruch, dass \(t-ξ_k\) für \(k \neq n\) Nullstellen aufweist und \(ξ_n - ξ_k\) das Polynom bei \(t = ξ_n\) auf \(1\) normiert, ergibt sich die Bedingung \[L_n(ξ_k) = \begin{cases} 1, & k = n, \\ 0, & k \neq n. \end{cases}\] Damit erhalten wir die Lagrange-Darstellung des Interpolationspolynoms \[P(t) = \sum_{n=0}^N f_nL_n(t)\]
⚠️ Probleme:
- Zusätzliche Stützstellen erfordern eine Neukonstruktion des gesamten Polynoms.
- Basis oszilliert stark
7.3 Newton-Darstellung
Wir betrachten Stützstellen \(\xi_1, \ldots, \xi_N\) und die zugehörigen Funktionswerte \(f(\xi_1), \ldots, f(\xi_N)\). Nach Newton-Schema rechnen wir die Koeffizienten \(c_n\) und bilden das Produkt mit dem jeweiligen Newton-Polynom \(\omega_n(t)\):
\[ P_N(t) = \sum_{n=0}^{N} c_n \cdot \omega_n(t) \quad \text{mit} \quad \omega_n(t) = \prod_{k=0}^{n-1} (t - \xi_k) \]
Alternativ lässt sich das Newton-Polynom \(\omega_n(t)\) auch rekursiv definieren:
\[ \omega_0(t) = 1, \quad \omega_n(t) = \omega_{n-1}(t) \cdot (t - \xi_{n-1}) \quad \text{für} \quad n = 1, \ldots, N. \]
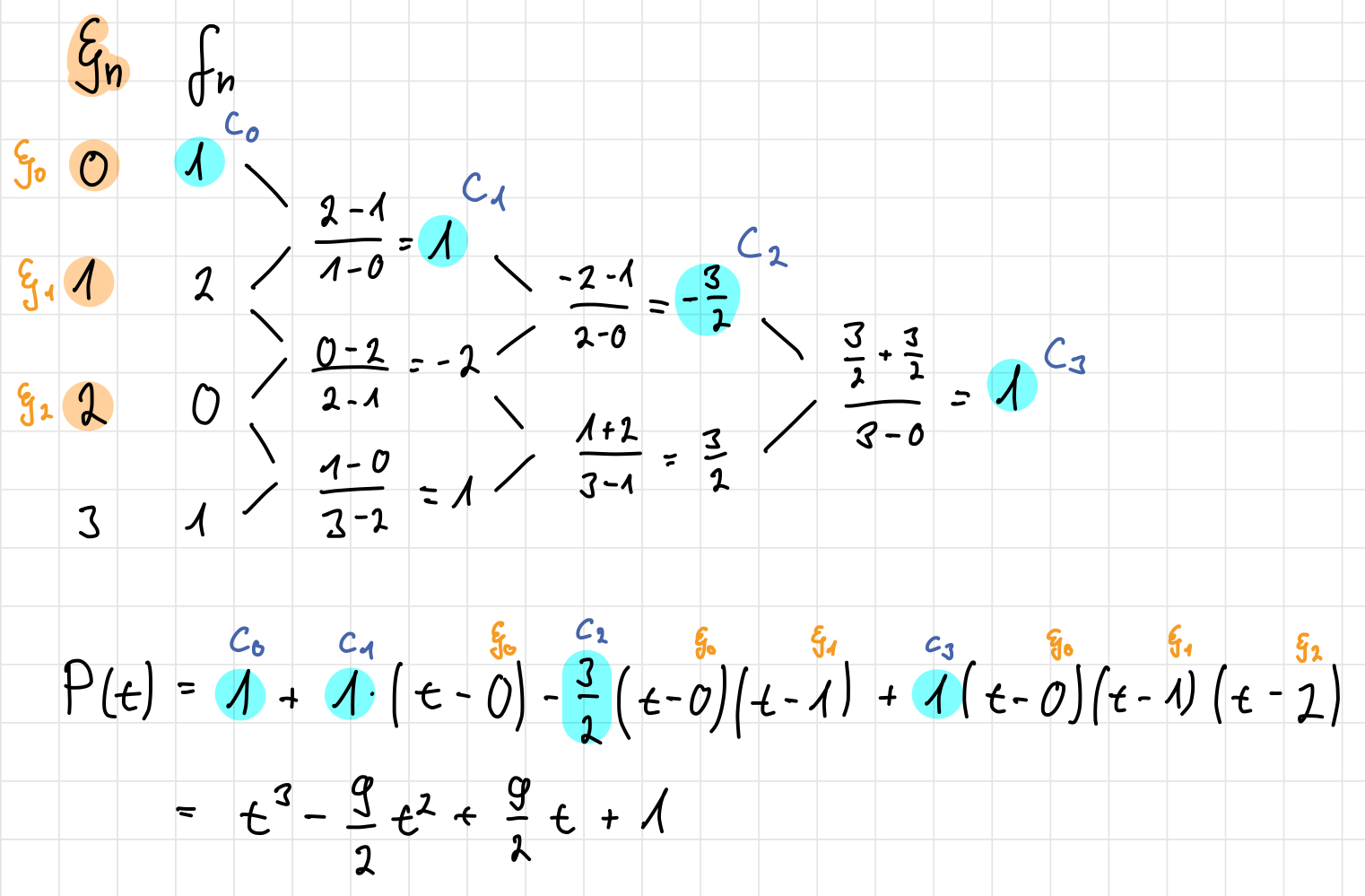
Sei \(f \in C^{N+1}[a,b]\) mit \(a < b\) und \(a \le t \le b\). Zu \(a \le \xi_0 \le \xi_1 \le \dots \le \xi_N \le b\) definiere \[ f_n = \frac{1}{e_n!} \left(\frac{d}{dt}\right)^{e_n} f(\xi_n). \]
Für den Interpolationsfehler gilt dann \[ f(t) - P_N(t) = \frac{\omega_{N+1}(t)}{(N+1)!} \left(\frac{d}{dt}\right)^{N+1} f(\tau_t) \] mit \(\tau_t \in I := [\min\{\xi_0, t\}, \max\{t, \xi_N\}]\).